微积分快速入门4部分:深入(极限、导数、定积分和不定积分)
9 无穷大(极限)
无穷大是一个既迷人又可怕的概念--有整整一门课(分析)都在研究它。我们将避免理论上的细微差别:我们的目标是切实理解无穷大如何帮助我们学习微积分。
9.1 启示: 有时可以测量无穷大
两个朋友相距 10 英里,分别以每小时 5 英里的速度相向而行。一只蚊子在他们之间快速飞过,先碰到一个人,然后碰到另一个人,一直碰到,直到朋友们击掌,蚊子被踩扁。
假设蚊子以每小时 20 英里的速度飞过。你能算出它在死亡前飞了多远吗?

呀 这个问题很棘手:一旦蚊子离开第一个人,碰到第二个人,然后转身......第一个人就已经靠近了!我们要把无数个不断缩小的距离加起来。这个问题似乎很难解决,对吗?
那么,这样推理如何:从步行者的角度来看,他们总共要走一个小时。毕竟,他们开始时相距 10 英里,而差距是以每小时 10 英里(5 英里+5 英里)的速度缩小的。因此,蚊子必须飞一小时,走 20 英里。
哇哦 我们刚刚找到了一个有无数步骤的过程的结果吗?我想是的!
9.2 将一个整体拆分为无限多个部分
是时候让我们的分步思维进入超速状态了。我们能把有限的图形分割成无限的部分吗?
蚊子的轨迹可以看作是一个整体,也可以看作是被细分为无数段的旅程。
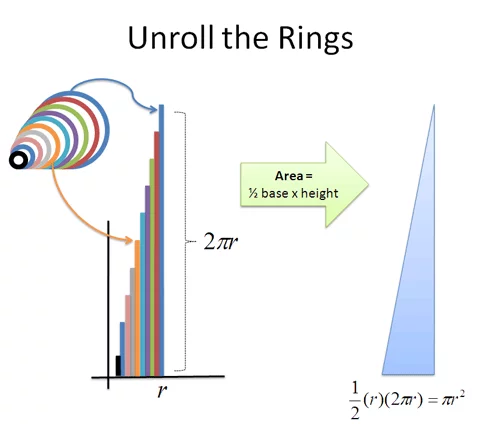
- 无限多的部分可以组合成有限的结果,只要它们减少的速度足够快
- 精度有限(但在不断提高)的过程与精度无限的过程可以得出相同的结果
- 用微积分的术语来说,这意味着从我们有限的(但不断增长的)步骤序列中得出的结论是可信的。
10 导数
上一课告诉我们,一连串无限的步骤可以得出有限的结论。让我们把它付诸实践,看看把变化分解成无限小的部分如何指向真正的数量。
10.1 类比: 测量心率
想象一下,你是一名医生,正试图测量病人运动时的心率。你把一个人放在跑步机上,绑上电极,让他跑步。机器显示每分钟心跳 180 次。这一定就是他的心率,对吗?
不是。这是他被医生观察时的心率,而且还带着电极。这种情况会不会很紧张?如果尼克松时代的电极缠在自己身上,在跑步时扯住他的腿怎么办?
啊。我们需要电极来进行测量。但紧接着,我们需要消除电极本身的影响。例如,如果我们测量的心率是 180 bpm,并且知道电极增加了 5 bpm 的压力,我们就会知道真实的心率是 175。
关键在于进行明知有误的测量,获得读数,然后进行修正,就好像仪器从未出现过一样。
10.2 测量导数
测量导数就像在函数上安装电极并使其运行一样。对于f(x)=x^2:
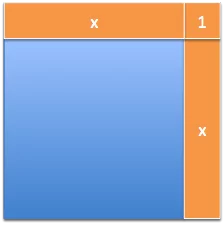
水平条纹是我们沿形状顶部施加变化的结果。垂直条纹是我们沿着侧面进行改变的结果。角落是什么呢?
它是水平变化与垂直变化相互作用的一部分!
10.3 丢弃人为结果
微积分的创始人凭直觉意识到哪些变化成分是 “人为的”,并直接将它们扔掉。他们发现,角片是我们的测试测量与自身相互作用的结果,不应该包括在内。
在现代,我们创造了关于如何做到这一点的官方理论:
- 极限: 我们让测量越来越小,直到它们有效消失(无法与零区分开来)。
- 无穷小: 创建一种新的数字类型,让我们在一个单独的微小数字系统中尝试无限小的变化。当我们把结果带回到我们的常规数系时,人为因素就会被去除。
有很多课程都在探讨这些理论。实际应用的结果是,认识到如何进行测量,然后扔掉我们不需要的部分。
下面是使用极限定义导数的方法:
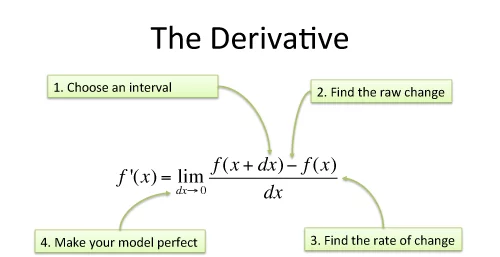
- 计算过程


参考资料
- 软件测试精品书籍文档下载持续更新 https://github.com/china-testing/python-testing-examples 请点赞,谢谢!
- 本文涉及的python测试开发库 谢谢点赞! https://github.com/china-testing/python_cn_resouce
- python精品书籍下载 https://github.com/china-testing/python_cn_resouce/blob/main/python_good_books.md
- Linux精品书籍下载 https://www.cnblogs.com/testing-/p/17438558.html
11 微积分基本定理 (FTOC The Fundamental Theorem Of Calculus)
11.1 第一部分:定积分的捷径
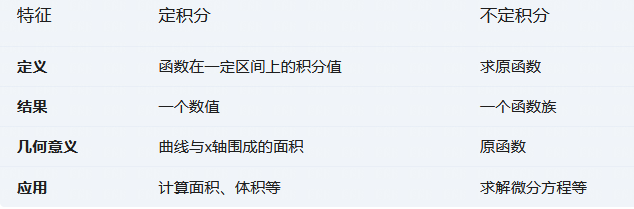
定积分表示函数在一定区间上的积分值,几何意义上代表函数曲线与x轴在该区间内围成的有符号面积。
如果导数和积分是对立的,我们就可以避开定积分中费力的积累过程。
例如,什么是 1 + 3 + 5 + 7 + 9?直接计算定积分的困难方法是直接将各项相加。(50 项怎么办?)

实际上就是等差数列。
下面是花哨语言的 FTOC 第一部分。如果我们有步数模式和原始模式,那么定积分的快捷方式就是:

定积分是一种粗略的机械计算,而不定积分是一个漂亮、简洁的公式。只要求出端点之间的差值,就能知道中间发生的事情的净结果!(有道理吧?)
11.2 第二部分:求不定积分
不定积分是求导的逆运算,即求原函数。
假设有某个原始函数(目前未知)可以跟踪累积:
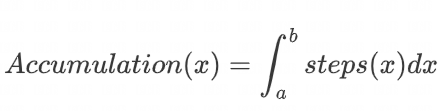
FTOC 指出,这个神奇函数的导数就是我们的步数:
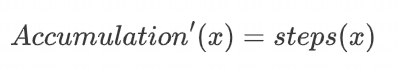
现在我们可以倒推。如果我们能找到某个随机函数,求出它的导数,并注意到它与我们的步数相匹配,我们就可以用这个函数作为我们的原始函数!
从技术上讲,导数等于当前步数的函数被称为反导数。2的一个反导是2x;另一个是2x+10.